Load Libraries and Helper Functions
library(Biostrings)
library(ape)
library(kSamples)
library(ggplot2)
library(gridExtra)
set.seed(201123) # For reproducibilityLeave-one-out density comparisons and Anderson–Darling null distribution generation
This analysis implements coincidence detection methods using genetic distances computed with the leave one out method.
The original simulation with random 40/160 splits, we generate ad_distribution and make helper distance functions for the splits.
# Function to compute within-sample minimum distances (excluding self-distances)
compute_within_sample_min_distances <- function(dist_mat, sample_indices) {
sample_dist_mat <- dist_mat[sample_indices, sample_indices]
min_distances <- apply(sample_dist_mat, 1, function(row) {
non_zero_distances <- row[row > 0] # Exclude self-distances (zeros)
if(length(non_zero_distances) > 0) {
return(min(non_zero_distances))
} else {
return(NA)
}
})
return(min_distances[!is.na(min_distances)]) # Remove any NAs
}
# Function to compute sample-to-population minimum distances
compute_sample_to_population_min_distances <- function(dist_mat, population_indices, sample_indices) {
# Distances from population to sample
pop_to_sample_dist_mat <- dist_mat[population_indices, sample_indices]
min_distances <- apply(pop_to_sample_dist_mat, 1, min)
return(min_distances)
}# Main simulation function
simulate_ad_statistics <- function(seqs, n_simulations = 500) {
# Compute distance matrix once
cat("Computing distance matrix...\n")
dist_matrix <- as.matrix(dist.dna(as.DNAbin(seqs), model = "K80", pairwise.deletion = TRUE))
ad_statistics <- numeric(n_simulations)
cat("Running", n_simulations, "simulations...\n")
for(i in 1:n_simulations) {
if(i %% 50 == 0) cat("Simulation", i, "of", n_simulations, "\n")
# Randomly split 200 sequences into sample (40) and population (160)
random_indices <- sample(nrow(dist_matrix), 200)
sample_indices <- random_indices[1:40]
population_indices <- random_indices[41:200]
# Compute within-sample minimum distances (n1 = up to 40, but typically 39 per point in this part)
within_sample_distances <- compute_within_sample_min_distances(dist_matrix, sample_indices)
# Compute sample-to-population minimum distances (n2 = 160)
sample_to_pop_distances <- compute_sample_to_population_min_distances(dist_matrix, population_indices, sample_indices)
# Compute Anderson-Darling statistic
if(length(within_sample_distances) > 0 && length(sample_to_pop_distances) > 0) {
ad_result <- ad.test(within_sample_distances, sample_to_pop_distances)
ad_statistics[i] <- ad_result$ad[1, 1]
} else {
ad_statistics[i] <- NA
}
}
# Remove any failed simulations
ad_statistics <- ad_statistics[!is.na(ad_statistics)]
cat("Completed", length(ad_statistics), "successful simulations\n")
return(ad_statistics)
}Computing distance matrix...
Running 500 simulations...
Simulation 50 of 500
Simulation 100 of 500
Simulation 150 of 500
Simulation 200 of 500
Simulation 250 of 500
Simulation 300 of 500
Simulation 350 of 500
Simulation 400 of 500
Simulation 450 of 500
Simulation 500 of 500
Completed 500 successful simulationsHere we are using our distance between and within functions to compare the leave one out for 40 point to the “true” distance computation for 160.
# The 4 selected simulations with density plots
# Show within-sample vs sample-to-population distances
# Save distance distributions for selected simulations
simulate_ad_statistics_with_distances <- function(seqs, n_simulations = 500, save_simulations = c(150, 200, 250, 450)) {
# Compute distance matrix once
cat("Computing distance matrix...\n")
dist_matrix <- as.matrix(dist.dna(as.DNAbin(seqs), model = "K80", pairwise.deletion = TRUE))
ad_statistics <- numeric(n_simulations)
saved_distances <- list()
cat("Running", n_simulations, "simulations...\n")
for(i in 1:n_simulations) {
if(i %% 50 == 0) cat("Simulation", i, "of", n_simulations, "\n")
# Randomly split 200 sequences into sample (40) and population (160)
random_indices <- sample(nrow(dist_matrix), 200)
sample_indices <- random_indices[1:40]
population_indices <- random_indices[41:200]
# Compute within-sample minimum distances (n1 = up to 40, but typically 39 per point)
within_sample_distances <- compute_within_sample_min_distances(dist_matrix, sample_indices)
# Compute sample-to-population minimum distances (n2 = 160)
sample_to_pop_distances <- compute_sample_to_population_min_distances(dist_matrix, population_indices, sample_indices)
# Save distances for selected simulations
if(i %in% save_simulations) {
saved_distances[[as.character(i)]] <- list(
within_sample = within_sample_distances,
sample_to_pop = sample_to_pop_distances
)
}
# Compute Anderson-Darling statistic
if(length(within_sample_distances) > 0 && length(sample_to_pop_distances) > 0) {
ad_result <- ad.test(within_sample_distances, sample_to_pop_distances)
ad_statistics[i] <- ad_result$ad[1, 1]
} else {
ad_statistics[i] <- NA
}
}
# Remove any failed simulations
ad_statistics <- ad_statistics[!is.na(ad_statistics)]
cat("Completed", length(ad_statistics), "successful simulations\n")
return(list(ad_statistics = ad_statistics, saved_distances = saved_distances))
}Computing distance matrix...
Running 500 simulations...
Simulation 50 of 500
Simulation 100 of 500
Simulation 150 of 500
Simulation 200 of 500
Simulation 250 of 500
Simulation 300 of 500
Simulation 350 of 500
Simulation 400 of 500
Simulation 450 of 500
Simulation 500 of 500
Completed 500 successful simulationsMake the comparison densities and the Anderson – Darling histogram for the 500 simulations of splits.
# Create density plots for the 4 selected simulations
library(gridExtra)
density_plots <- list()
for(i in 1:length(saved_distances)) {
sim_num <- names(saved_distances)[i]
within_dist <- saved_distances[[sim_num]]$within_sample
between_dist <- saved_distances[[sim_num]]$sample_to_pop
# Create combined data frame
plot_data <- data.frame(
distance = c(within_dist, between_dist),
type = factor(c(rep("Within-Sample", length(within_dist)),
rep("Sample-to-Population", length(between_dist))))
)
# Calculate AD statistic for this simulation
ad_stat <- round(ad_distribution[as.numeric(sim_num)], 3)
density_plots[[i]] <- ggplot(plot_data, aes(x = distance, fill = type)) +
geom_density(alpha = 0.6) +
scale_fill_manual(values = c("Within-Sample" = "blue", "Sample-to-Population" = "red")) +
labs(#title = paste("Simulation", sim_num, "- AD =", ad_stat),
x = "Minimum Distance",
y = "Density",
fill = "Distance Type") +
theme_minimal() +
theme(legend.position = "none")
}
# Arrange the 4 density plots in a 2x2 grid
combined_density_plot <- grid.arrange(density_plots[[1]], density_plots[[2]],
density_plots[[3]], density_plots[[4]],
ncol = 2, nrow = 2)
TableGrob (2 x 2) "arrange": 4 grobs
z cells name grob
1 1 (1-1,1-1) arrange gtable[layout]
2 2 (1-1,2-2) arrange gtable[layout]
3 3 (2-2,1-1) arrange gtable[layout]
4 4 (2-2,2-2) arrange gtable[layout]
Summary of AD Statistics:Mean: 1.545891 Median: 1.21445 95th Percentile: 3.874305 Standard Deviation: 1.085291
AD Statistics for selected simulations:Simulation 150 : AD = 0.867
Simulation 200 : AD = 1.0111
Simulation 250 : AD = 2.4349
Simulation 450 : AD = 3.6647 # Create the histogram for Figure 7b, no title
hist_plot_nt <- ggplot(data.frame(ad_statistic = ad_distribution), aes(x = ad_statistic)) +
geom_histogram(binwidth = 0.2, fill = "lightblue", color = "darkblue", alpha = 0.7) +
geom_vline(aes(xintercept = median(ad_statistic)), color = "darkblue", linetype = "dashed", size = 1) +
geom_vline(aes(xintercept = quantile(ad_statistic, 0.95)), color = "purple", linetype = "dashed", size = 1) +
labs(x = "Anderson-Darling Statistic",
y = "Frequency") +
theme_minimal() +
annotate("text", x = median(ad_distribution)+0.6, y = 60,
label = paste("Median =", round(median(ad_distribution), 2)), vjust = 1, color = "darkblue") +
annotate("text", x = quantile(ad_distribution, 0.95), y = max(table(cut(ad_distribution, breaks = 20)))*0.1,
label = paste("95th % =", round(quantile(ad_distribution, 0.95), 2)), vjust = -1, color = "purple")
print(hist_plot_nt)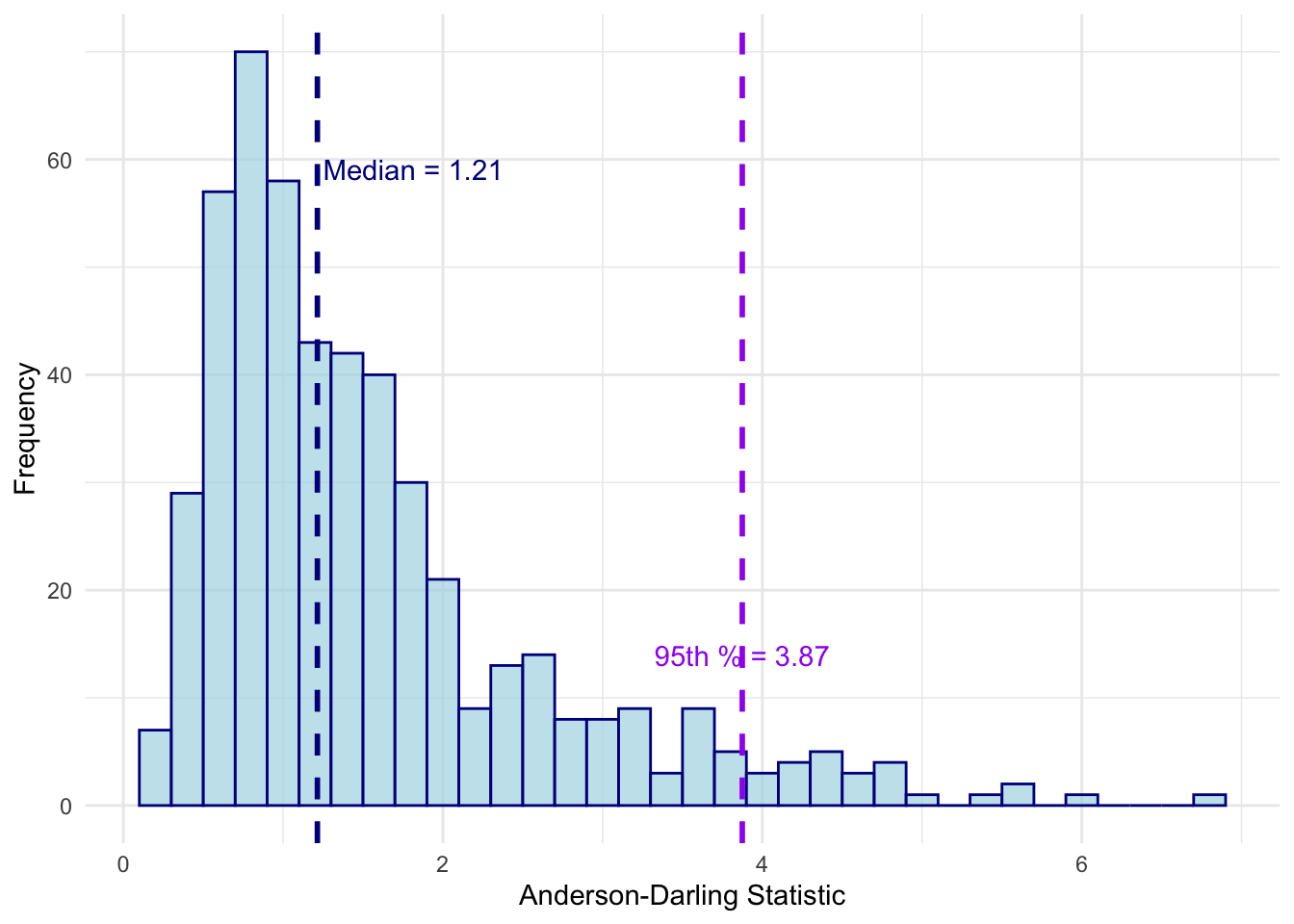
# Bootstrap + mutate to create 1000-sequence population
# Function to bootstrap and mutate sequences (your existing code)
bootstrap_and_mutate_sequences <- function(seqs, n, mutation_rate = 0.01) {
bootstrapped_seqs <- sample(seqs, n, replace = TRUE)
mutated_seqs <- sapply(bootstrapped_seqs, function(seq) {
seq_vector <- strsplit(as.character(seq), "")[[1]]
mutation_sites <- which(runif(length(seq_vector)) < mutation_rate)
seq_vector[mutation_sites] <- sample(c("A", "C", "G", "T"), length(mutation_sites), replace = TRUE)
paste(seq_vector, collapse = "")
})
return(DNAStringSet(mutated_seqs))
}Null from 40 random to 40 random and 160 random to 40 random
# Function to generate the clean null distribution (all independent random sets)
generate_clean_null_ad_distribution <- function(metapopulation_seqs, n_simulations = 500) {
# Compute distance matrix for the entire metapopulation once
cat("Computing distance matrix for metapopulation...\n")
dist_matrix <- as.matrix(dist.dna(as.DNAbin(metapopulation_seqs), model = "K80", pairwise.deletion = TRUE))
clean_null_ad_statistics <- numeric(n_simulations)
cat("Generating clean null distribution with", n_simulations, "simulations...\n")
for(i in 1:n_simulations) {
if(i %% 50 == 0) cat("Clean null simulation", i, "of", n_simulations, "\n")
# Draw four independent random sets from metapopulation
# Set 1: 40 random points (group 1)
random_40_group1 <- sample(nrow(dist_matrix), 40)
# Set 2: 40 different random points (target for group 1)
remaining_indices <- setdiff(1:nrow(dist_matrix), random_40_group1)
random_40_target1 <- sample(remaining_indices, 40)
# Set 3: 160 different random points (group 2)
remaining_indices_2 <- setdiff(remaining_indices, random_40_target1)
random_160_group2 <- sample(remaining_indices_2, 160)
# Set 4: 40 fresh different random points (target for group 2)
remaining_indices_3 <- setdiff(remaining_indices_2, random_160_group2)
random_40_target2 <- sample(remaining_indices_3, 40)
# Compute distances: 40 random → 40 random target (set 1)
group1_to_target_distances <- compute_sample_to_population_min_distances(
dist_matrix, random_40_group1, random_40_target1)
# Compute distances: 160 random → different 40 random target (set 2)
group2_to_target_distances <- compute_sample_to_population_min_distances(
dist_matrix, random_160_group2, random_40_target2)
# Compute Anderson-Darling statistic
if(length(group1_to_target_distances) > 0 && length(group2_to_target_distances) > 0) {
ad_result <- ad.test(group1_to_target_distances, group2_to_target_distances)
clean_null_ad_statistics[i] <- ad_result$ad[1, 1]
} else {
clean_null_ad_statistics[i] <- NA
}
}
# Remove any failed simulations
clean_null_ad_statistics <- clean_null_ad_statistics[!is.na(clean_null_ad_statistics)]
cat("Completed", length(clean_null_ad_statistics), "successful clean null simulations\n")
return(clean_null_ad_statistics)
}
# Generate the clean null distribution
clean_null_ad_distribution <- generate_clean_null_ad_distribution(population_seqs, n_simulations = 500)Computing distance matrix for metapopulation...
Generating clean null distribution with 500 simulations...
Clean null simulation 50 of 500
Clean null simulation 100 of 500
Clean null simulation 150 of 500
Clean null simulation 200 of 500
Clean null simulation 250 of 500
Clean null simulation 300 of 500
Clean null simulation 350 of 500
Clean null simulation 400 of 500
Clean null simulation 450 of 500
Clean null simulation 500 of 500
Completed 500 successful clean null simulationsThis is the plot we show in the Figure.
# Create comparison plot
comparison_plot <- ggplot(comparison_data, aes(x = AD_Statistic, fill = Distribution)) +
geom_density(alpha = 0.6) +
scale_fill_manual(values = c("Leave one out split 200" = "blue",
"Null all independent" = "red")) +
labs(#title = "Clean Comparison: Original Data Split vs Fully Independent Random Null",
x = "Anderson-Darling Statistic",
y = "Density",
fill = "Distribution Type") +
theme_minimal() +
theme(legend.position = "bottom")
print(comparison_plot)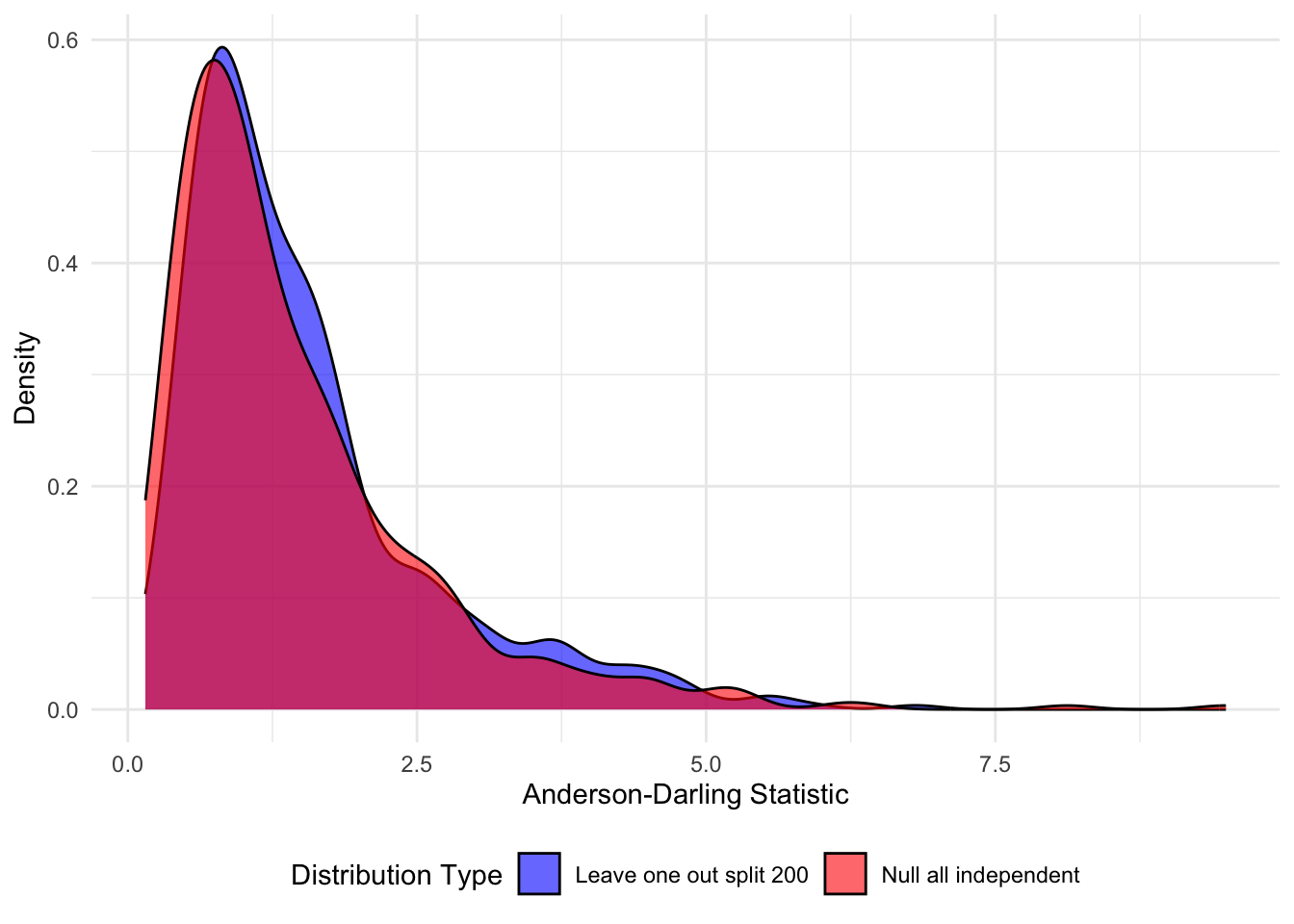
Clean Comparison (Fully Independent):Original Data Split - Mean: 1.5459 , Median: 1.2145 , 95th percentile: 3.8743 Clean Null - Mean: 1.4584 , Median: 1.0966 , 95th percentile: 3.7428 Proportion of original AD statistics exceeding clean null 95th percentile: 0.054 Estimated p-value for test: 0.054 # Compare ad_distribution vs clean_null_ad_distribution
# Create QQ plot data
qq_data <- data.frame(
clean_null = sort(clean_null_ad_distribution),
original_split = sort(ad_distribution)
)
# Create QQ plot
qq_plot <- ggplot(qq_data, aes(x = clean_null, y = original_split)) +
geom_point(alpha = 0.6) +
geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed",linewidth=1.5) +
labs(x = "Null Distribution AD Quantiles",
y = "Data Split AD Quantiles") +
theme_minimal()
print(qq_plot)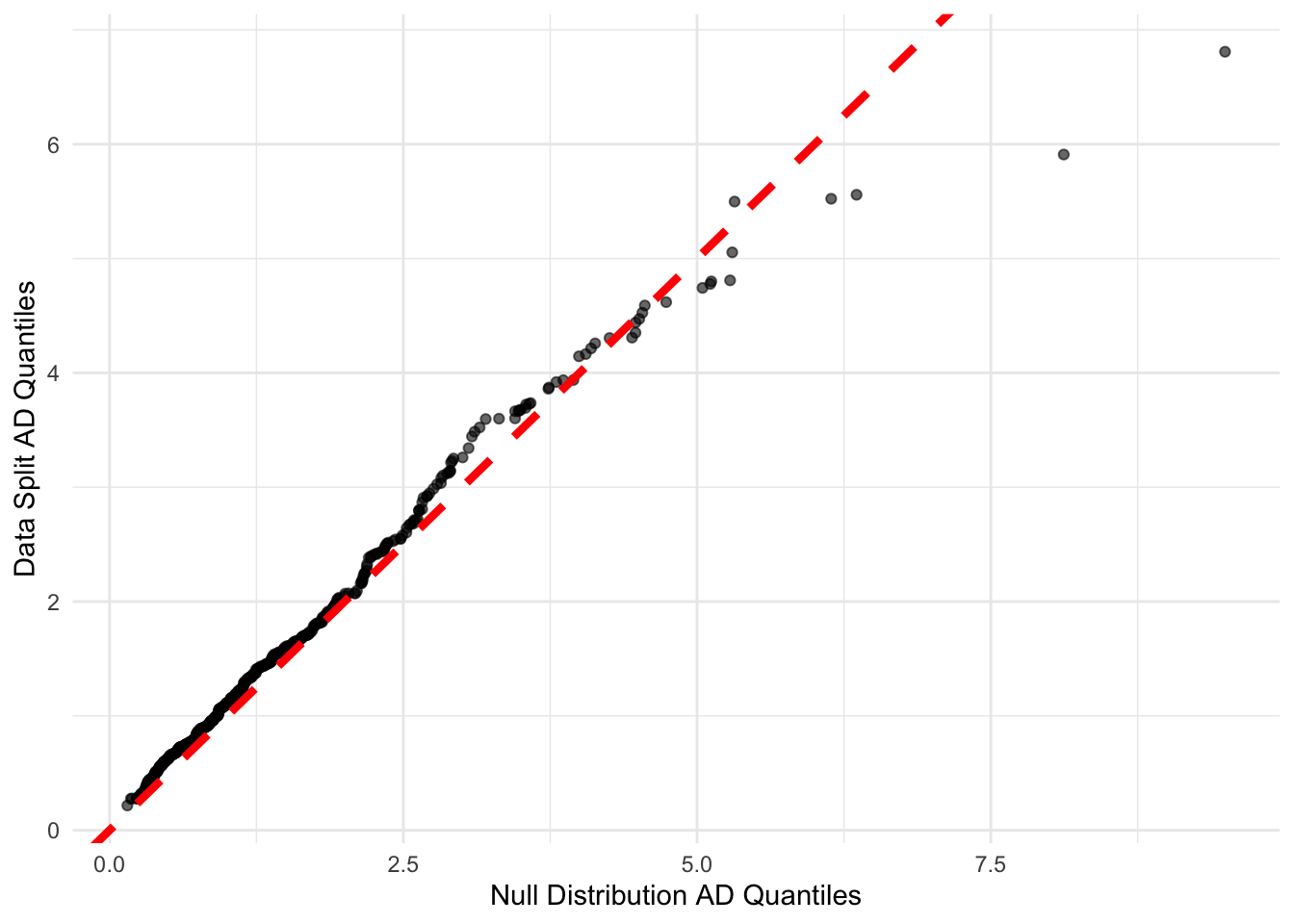
---
title: "Coincidence Detection using Distances: Simulations"
subtitle: "Leave-one-out density comparisons and Anderson--Darling null distribution generation"
execute:
warning: false
message: false
cache: false
---
## Overview
This analysis implements coincidence detection methods using genetic distances computed with the leave one out method.
## Setup
```{r setup}
#| code-fold: true
#| code-summary: "Load Libraries and Helper Functions"
library(Biostrings)
library(ape)
library(kSamples)
library(ggplot2)
library(gridExtra)
set.seed(201123) # For reproducibility
```
```{r load_data}
# Read the data
aligned_seqs <- readDNAStringSet("../data/silva_aligned_bacteria_sequences.fasta")
cat("Loaded", length(aligned_seqs), "sequences\n")
```
## Part 1: Random Split Analysis
The original simulation with random 40/160 splits, we
generate `ad_distribution` and make helper distance functions for
the splits.
```{r distancefunctions}
#| code-fold: true
# Function to compute within-sample minimum distances (excluding self-distances)
compute_within_sample_min_distances <- function(dist_mat, sample_indices) {
sample_dist_mat <- dist_mat[sample_indices, sample_indices]
min_distances <- apply(sample_dist_mat, 1, function(row) {
non_zero_distances <- row[row > 0] # Exclude self-distances (zeros)
if(length(non_zero_distances) > 0) {
return(min(non_zero_distances))
} else {
return(NA)
}
})
return(min_distances[!is.na(min_distances)]) # Remove any NAs
}
# Function to compute sample-to-population minimum distances
compute_sample_to_population_min_distances <- function(dist_mat, population_indices, sample_indices) {
# Distances from population to sample
pop_to_sample_dist_mat <- dist_mat[population_indices, sample_indices]
min_distances <- apply(pop_to_sample_dist_mat, 1, min)
return(min_distances)
}
```
```{r mainsimulation}
# Main simulation function
simulate_ad_statistics <- function(seqs, n_simulations = 500) {
# Compute distance matrix once
cat("Computing distance matrix...\n")
dist_matrix <- as.matrix(dist.dna(as.DNAbin(seqs), model = "K80", pairwise.deletion = TRUE))
ad_statistics <- numeric(n_simulations)
cat("Running", n_simulations, "simulations...\n")
for(i in 1:n_simulations) {
if(i %% 50 == 0) cat("Simulation", i, "of", n_simulations, "\n")
# Randomly split 200 sequences into sample (40) and population (160)
random_indices <- sample(nrow(dist_matrix), 200)
sample_indices <- random_indices[1:40]
population_indices <- random_indices[41:200]
# Compute within-sample minimum distances (n1 = up to 40, but typically 39 per point in this part)
within_sample_distances <- compute_within_sample_min_distances(dist_matrix, sample_indices)
# Compute sample-to-population minimum distances (n2 = 160)
sample_to_pop_distances <- compute_sample_to_population_min_distances(dist_matrix, population_indices, sample_indices)
# Compute Anderson-Darling statistic
if(length(within_sample_distances) > 0 && length(sample_to_pop_distances) > 0) {
ad_result <- ad.test(within_sample_distances, sample_to_pop_distances)
ad_statistics[i] <- ad_result$ad[1, 1]
} else {
ad_statistics[i] <- NA
}
}
# Remove any failed simulations
ad_statistics <- ad_statistics[!is.na(ad_statistics)]
cat("Completed", length(ad_statistics), "successful simulations\n")
return(ad_statistics)
}
```
```{r runsimulationsplits}
# Run the simulations
# This was the original one
ad_distribution <- simulate_ad_statistics(aligned_seqs, n_simulations = 500)
```
## Part 2: Distance Distributions Comparison and AD computation
Here we are using our distance between and within functions to
compare the leave one out for 40 point to the "true" distance computation for 160.
```{r distance-comparisons}
# The 4 selected simulations with density plots
# Show within-sample vs sample-to-population distances
# Save distance distributions for selected simulations
simulate_ad_statistics_with_distances <- function(seqs, n_simulations = 500, save_simulations = c(150, 200, 250, 450)) {
# Compute distance matrix once
cat("Computing distance matrix...\n")
dist_matrix <- as.matrix(dist.dna(as.DNAbin(seqs), model = "K80", pairwise.deletion = TRUE))
ad_statistics <- numeric(n_simulations)
saved_distances <- list()
cat("Running", n_simulations, "simulations...\n")
for(i in 1:n_simulations) {
if(i %% 50 == 0) cat("Simulation", i, "of", n_simulations, "\n")
# Randomly split 200 sequences into sample (40) and population (160)
random_indices <- sample(nrow(dist_matrix), 200)
sample_indices <- random_indices[1:40]
population_indices <- random_indices[41:200]
# Compute within-sample minimum distances (n1 = up to 40, but typically 39 per point)
within_sample_distances <- compute_within_sample_min_distances(dist_matrix, sample_indices)
# Compute sample-to-population minimum distances (n2 = 160)
sample_to_pop_distances <- compute_sample_to_population_min_distances(dist_matrix, population_indices, sample_indices)
# Save distances for selected simulations
if(i %in% save_simulations) {
saved_distances[[as.character(i)]] <- list(
within_sample = within_sample_distances,
sample_to_pop = sample_to_pop_distances
)
}
# Compute Anderson-Darling statistic
if(length(within_sample_distances) > 0 && length(sample_to_pop_distances) > 0) {
ad_result <- ad.test(within_sample_distances, sample_to_pop_distances)
ad_statistics[i] <- ad_result$ad[1, 1]
} else {
ad_statistics[i] <- NA
}
}
# Remove any failed simulations
ad_statistics <- ad_statistics[!is.na(ad_statistics)]
cat("Completed", length(ad_statistics), "successful simulations\n")
return(list(ad_statistics = ad_statistics, saved_distances = saved_distances))
}
```
```{r}
# Run the simulations with distance saving
results <- simulate_ad_statistics_with_distances(aligned_seqs, n_simulations = 500,
save_simulations = c(150, 200, 250, 450))
ad_distribution <- results$ad_statistics
saved_distances <- results$saved_distances
```
### Plots comparing four of the distance pairs for Figure 7a
Make the comparison densities and the Anderson -- Darling histogram for the 500
simulations of splits.
```{r simul4}
#| fig-cap: "Four exemplary simulations and the two densities compared."
# Create density plots for the 4 selected simulations
library(gridExtra)
density_plots <- list()
for(i in 1:length(saved_distances)) {
sim_num <- names(saved_distances)[i]
within_dist <- saved_distances[[sim_num]]$within_sample
between_dist <- saved_distances[[sim_num]]$sample_to_pop
# Create combined data frame
plot_data <- data.frame(
distance = c(within_dist, between_dist),
type = factor(c(rep("Within-Sample", length(within_dist)),
rep("Sample-to-Population", length(between_dist))))
)
# Calculate AD statistic for this simulation
ad_stat <- round(ad_distribution[as.numeric(sim_num)], 3)
density_plots[[i]] <- ggplot(plot_data, aes(x = distance, fill = type)) +
geom_density(alpha = 0.6) +
scale_fill_manual(values = c("Within-Sample" = "blue", "Sample-to-Population" = "red")) +
labs(#title = paste("Simulation", sim_num, "- AD =", ad_stat),
x = "Minimum Distance",
y = "Density",
fill = "Distance Type") +
theme_minimal() +
theme(legend.position = "none")
}
# Arrange the 4 density plots in a 2x2 grid
combined_density_plot <- grid.arrange(density_plots[[1]], density_plots[[2]],
density_plots[[3]], density_plots[[4]],
ncol = 2, nrow = 2)
combined_density_plot
# Save the combined plot for Figure left side
# ggsave("four_density_comparisons.png", combined_density_plot, width = 4, height = 4, dpi = 300)
# Summary statistics
cat("\nSummary of AD Statistics:\n")
cat("Mean:", mean(ad_distribution), "\n")
cat("Median:", median(ad_distribution), "\n")
cat("95th Percentile:", quantile(ad_distribution, 0.95), "\n")
cat("Standard Deviation:", sd(ad_distribution), "\n")
# Print AD statistics for the selected simulations
cat("\nAD Statistics for selected simulations:\n")
for(sim_num in names(saved_distances)) {
cat("Simulation", sim_num, ": AD =", round(ad_distribution[as.numeric(sim_num)], 4), "\n")
}
```
### Histogram of Anderson --Darling 500 stats for 7b
```{r hist7b}
#| fig-cap: "Histogram of the 500 Anderson--Statistic comparing the 40 LOO distances and the 160 sample to population ones."
# Create the histogram for Figure 7b, no title
hist_plot_nt <- ggplot(data.frame(ad_statistic = ad_distribution), aes(x = ad_statistic)) +
geom_histogram(binwidth = 0.2, fill = "lightblue", color = "darkblue", alpha = 0.7) +
geom_vline(aes(xintercept = median(ad_statistic)), color = "darkblue", linetype = "dashed", size = 1) +
geom_vline(aes(xintercept = quantile(ad_statistic, 0.95)), color = "purple", linetype = "dashed", size = 1) +
labs(x = "Anderson-Darling Statistic",
y = "Frequency") +
theme_minimal() +
annotate("text", x = median(ad_distribution)+0.6, y = 60,
label = paste("Median =", round(median(ad_distribution), 2)), vjust = 1, color = "darkblue") +
annotate("text", x = quantile(ad_distribution, 0.95), y = max(table(cut(ad_distribution, breaks = 20)))*0.1,
label = paste("95th % =", round(quantile(ad_distribution, 0.95), 2)), vjust = -1, color = "purple")
print(hist_plot_nt)
# ggsave("ADhistogram.png",hist_plot_nt,width=5,height=4)
```
## Part 3: Null Distribution of Anderson--Darling : Generation
```{r null-generation}
#| code-fold: true
# Bootstrap + mutate to create 1000-sequence population
# Function to bootstrap and mutate sequences (your existing code)
bootstrap_and_mutate_sequences <- function(seqs, n, mutation_rate = 0.01) {
bootstrapped_seqs <- sample(seqs, n, replace = TRUE)
mutated_seqs <- sapply(bootstrapped_seqs, function(seq) {
seq_vector <- strsplit(as.character(seq), "")[[1]]
mutation_sites <- which(runif(length(seq_vector)) < mutation_rate)
seq_vector[mutation_sites] <- sample(c("A", "C", "G", "T"), length(mutation_sites), replace = TRUE)
paste(seq_vector, collapse = "")
})
return(DNAStringSet(mutated_seqs))
}
```
### Create metapopulation
```{r metapop}
population_size <- 1000
cat("Creating metapopulation of", population_size, "sequences...\n")
population_seqs <- bootstrap_and_mutate_sequences(aligned_seqs, population_size, mutation_rate = 0.01)
```
### Generate clean_null_ad_distribution with independent samples
Null from 40 random to 40 random and 160 random to 40 random
```{r generatenull}
#| code-fold: true
# Function to generate the clean null distribution (all independent random sets)
generate_clean_null_ad_distribution <- function(metapopulation_seqs, n_simulations = 500) {
# Compute distance matrix for the entire metapopulation once
cat("Computing distance matrix for metapopulation...\n")
dist_matrix <- as.matrix(dist.dna(as.DNAbin(metapopulation_seqs), model = "K80", pairwise.deletion = TRUE))
clean_null_ad_statistics <- numeric(n_simulations)
cat("Generating clean null distribution with", n_simulations, "simulations...\n")
for(i in 1:n_simulations) {
if(i %% 50 == 0) cat("Clean null simulation", i, "of", n_simulations, "\n")
# Draw four independent random sets from metapopulation
# Set 1: 40 random points (group 1)
random_40_group1 <- sample(nrow(dist_matrix), 40)
# Set 2: 40 different random points (target for group 1)
remaining_indices <- setdiff(1:nrow(dist_matrix), random_40_group1)
random_40_target1 <- sample(remaining_indices, 40)
# Set 3: 160 different random points (group 2)
remaining_indices_2 <- setdiff(remaining_indices, random_40_target1)
random_160_group2 <- sample(remaining_indices_2, 160)
# Set 4: 40 fresh different random points (target for group 2)
remaining_indices_3 <- setdiff(remaining_indices_2, random_160_group2)
random_40_target2 <- sample(remaining_indices_3, 40)
# Compute distances: 40 random → 40 random target (set 1)
group1_to_target_distances <- compute_sample_to_population_min_distances(
dist_matrix, random_40_group1, random_40_target1)
# Compute distances: 160 random → different 40 random target (set 2)
group2_to_target_distances <- compute_sample_to_population_min_distances(
dist_matrix, random_160_group2, random_40_target2)
# Compute Anderson-Darling statistic
if(length(group1_to_target_distances) > 0 && length(group2_to_target_distances) > 0) {
ad_result <- ad.test(group1_to_target_distances, group2_to_target_distances)
clean_null_ad_statistics[i] <- ad_result$ad[1, 1]
} else {
clean_null_ad_statistics[i] <- NA
}
}
# Remove any failed simulations
clean_null_ad_statistics <- clean_null_ad_statistics[!is.na(clean_null_ad_statistics)]
cat("Completed", length(clean_null_ad_statistics), "successful clean null simulations\n")
return(clean_null_ad_statistics)
}
# Generate the clean null distribution
clean_null_ad_distribution <- generate_clean_null_ad_distribution(population_seqs, n_simulations = 500)
# Compare clean null vs original data split
comparison_data <- data.frame(
AD_Statistic = c(ad_distribution, clean_null_ad_distribution),
Distribution = factor(c(rep("Leave one out split 200", length(ad_distribution)),
rep("Null all independent", length(clean_null_ad_distribution))))
)
```
### Compare the densities of the 500 random splits AD to the null generated above
This is the plot we show in the Figure.
```{r}
#| fig-cap: "Comparison: Original Data Split vs Fully Independent Random Null"
# Create comparison plot
comparison_plot <- ggplot(comparison_data, aes(x = AD_Statistic, fill = Distribution)) +
geom_density(alpha = 0.6) +
scale_fill_manual(values = c("Leave one out split 200" = "blue",
"Null all independent" = "red")) +
labs(#title = "Clean Comparison: Original Data Split vs Fully Independent Random Null",
x = "Anderson-Darling Statistic",
y = "Density",
fill = "Distribution Type") +
theme_minimal() +
theme(legend.position = "bottom")
print(comparison_plot)
# Summary statistics comparison
cat("\nClean Comparison (Fully Independent):\n")
cat("Original Data Split - Mean:", round(mean(ad_distribution), 4),
", Median:", round(median(ad_distribution), 4),
", 95th percentile:", round(quantile(ad_distribution, 0.95), 4), "\n")
cat("Clean Null - Mean:", round(mean(clean_null_ad_distribution), 4),
", Median:", round(median(clean_null_ad_distribution), 4),
", 95th percentile:", round(quantile(clean_null_ad_distribution, 0.95), 4), "\n")
# Calculate p-value
clean_null_95th <- quantile(clean_null_ad_distribution, 0.95)
proportion_exceeding_clean_null <- mean(ad_distribution > clean_null_95th)
cat("Proportion of original AD statistics exceeding clean null 95th percentile:",
round(proportion_exceeding_clean_null, 4), "\n")
# This gives you a clean p-value for testing population structure
cat("Estimated p-value for test:", round(proportion_exceeding_clean_null, 4), "\n")
# Save the comparison plot without the legend
# ggsave("ad_fully_independent_comparison.png", comparison_plot_nt, width = 6, height = 4, dpi = 300)
```
## Part 4: Final Comparison through a quantile-quantile plot
```{r final-comparison}
#| fig-cap: "QQ plot for AD with null on x axis and data split AD on y."
# Compare ad_distribution vs clean_null_ad_distribution
# Create QQ plot data
qq_data <- data.frame(
clean_null = sort(clean_null_ad_distribution),
original_split = sort(ad_distribution)
)
# Create QQ plot
qq_plot <- ggplot(qq_data, aes(x = clean_null, y = original_split)) +
geom_point(alpha = 0.6) +
geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed",linewidth=1.5) +
labs(x = "Null Distribution AD Quantiles",
y = "Data Split AD Quantiles") +
theme_minimal()
print(qq_plot)
# Save the QQ plot
# ggsave("qq_plot_null_vs_original.png", qq_plot, width = 4, height = 4, dpi = 300)
```